photolithography(포토리소그래피) 공정_Expose(2)
Expose(2)_NA, DOF, Resolution
바로 이전 글에서 Expose공정 시 렌즈의 크기가 Na와 관련되어 있고 더 큰 렌즈를 사용해야 한다고 했습니다. 그 이유에 대해 알아보겠습니다.
본격적으로 들어가기 전 빛의 성질인 회절에 대해 알아보겠습니다.
기초물리학의 Young의 이중슬릿 실험은 아래와 같습니다.

위 그림에서 monochromatic planar wave가 빛, screen with two slit이 Mask. optical screen이 Wafer라고 생각해 보겠습니다.
*실제 Mask는 저거보다 틈이 매우 많은 복잡한 회로로 구성이 되어 있습니다.
빛이 Mask를 통과할 때 Cr으로 막은 부분을 제외한 틈에 빛이 통과되어 Wafer위에 투영됩니다. 위와 같이 빛이 Mask를 통과할 때, Mask 틈 사이를 지난 빛이, 일직선으로 Wafer위로 투영되지 않는 모습을 볼 수 있습니다. 이는 빛의 회절이라는 성질 때문입니다. 회절 현상으로 인해 Mask 사이 틈을 통과 후, 반원 모양의 파동으로 퍼져가며 진행이 되고, 틈이 2개라면 위 그림과 같이 파동이 중첩되어 wafer위에 전사가 됩니다. 이를 보강간섭이라고 하며, 보강간섭 된 부분은 mask의 회로 정보를 담고 있습니다. n=0은 0차광, n=1은 1차광이라고 합니다. 반대로 n=0 아래, 다음 빛의 파동이 중첩되는 곳은 n=-1, 즉 -1차광이 됩니다.
저번 시간에 투사 노광법을 배우며 Mask는 렌즈 사이에 있다고 알게 되었습니다. 그래서 실제로는 Mask를 통과한 빛이 위 그림처럼 바로 wafer위에 투영되지 않고, 볼록렌즈를 거쳐 축소 노광이 됩니다. 따라서 Mask를 통과한 회절된 빛이 최대한 많이 볼록렌즈에 통과되어 wafer위에 투영되어야 합니다. 그러기 위해서는 0차광~n차광 등 최대한 많은 차광이 볼록렌즈에 들어가야 한다는 것을 알 수 있습니다.
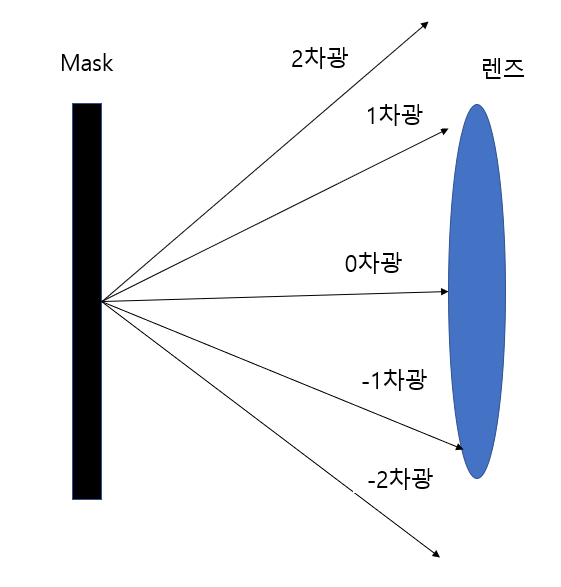
어떻게 해야 많은 차광의 빛을 담을 수 있을까요?
첫번째로 회절각을 줄여야 하고, 두번째로 렌즈의 크기를 크게 해야합니다.
빛이 틈을 지나 퍼지는 것을 보았습니다. 그 퍼지는 각도를 회절각이라고 합니다.
(1) Mask의 틈이 작을수록 회절각은 넓어집니다.
(2) 사용하는 빛의 파장이 장파장일 수록 회절각은 넓어집니다.
회절각이 넓어진다는 의미는 빛의 보강간섭이 일어나는 0차광과 1차광 사이의 거리가 멀어진다는 의미입니다. 이 거리가 멀어지면 mask를 통과한 회절 된 빛의 많은 차광들이 렌즈를 통과할 수 없겠죠? (여기서 렌즈의 크기가 커야 한다는 사실을 이해하실 수 있을겁니다.)
하지만 반도체 소자의 미세화로 인해 Mask의 틈은 갈수록 줄어들고 있고, 이에 따라 회절현상도 심화되고 있습니다. 회절 현상을 줄이기 위해 아래와 같은 방법이 있습니다.
(1) 파장이 작은 광원 사용.
(2) 퍼져나가는 회절광을 최대한 통과시킬 수 있는 큰 렌즈(Na)의 사용.
정리하자면 파장이 작은 광원을 사용해 회절각을 줄이고, 큰 렌즈를 사용해 많은 차광의 빛을 통과시켜야 하는 것입니다.
NA(Numerical Aperture)란?
드디어 NA가 나왔네요. NA는 렌즈의 크기를 의미하고 퍼져나가는 빛의 정보를 최대한 담기 위해 큰 렌즈가 필요한 것이었습니다. 이는 해상도가 좋아짐을 의미합니다.
지금부터는 NA에 대해 자세히 알아보고 그와 연관된 DOF, Resolution(해상도)에 대해 알아보겠습니다.

NA가 왜 렌즈의 크기를 의미할까요?
위 그림은 마스크를 통과한 회절 빛이 렌즈를 통과 후 wafer에 전사되는 모습입니다.
NA = n*sinΘ 를 의미하고 여기서 n은 굴절률을 의미합니다. NA가 왜 렌즈의 크기를 의미할까요? 수학적으로 계산해 보겠습니다. 렌즈와 wafer사이의 거리가 멀어 각도 세타가 작다고 가정하겠습니다. 그렇다면 sin세타는 tan세타로 근사시킬 수 있습니다. n*sin세타=n*tan세타=n*(r/F). 여기서 F를 고정하면 Na는 렌즈의 반지름인 r과 비례하겠죠? 그래서 NA를 렌즈의 크기를 의미한다고 말합니다.
NA = n*sinΘ 에서 n(굴절률)은 언제 바뀔까요?
n은 렌즈와 wafer사이 매질에 따라 바뀝니다. 보통 wafer와 렌즈 사이는 진공이기에 굴절률 n은 1입니다. 최근 기술로는 렌즈와 wafer사이에 물을 넣어 n값을 늘리는 immersion장비가 개발되어 사용되고 있습니다. 물을 넣는 기술은 다음 글에 후술 하겠습니다.
해상도(Resolution)
해상도란 wafer상에 전사시킬 수 있는 최소 패턴의 크기입니다. 위 그림에서 R(해상도)라고 적혀있듯이 말이죠.
*마찬가지로 R(해상도) 길이는 좀 과장해서 크게 표시했습니다. 실제로는 nm단위입니다.
따라서 해상도는 패턴의 크기가 작을수록 좋은 것이므로 R 또한 작을수록 좋습니다.
왜 패턴의 크기가 작을수록 좋을까요? 동일한 면적에 더 많은 회로 패턴을 넣을 수 있기 때문입니다.
지금까지 종합해보면 해상도 R은 렌즈의 크기가 클수록 더 많은 차광의 빛을 담을 수 있고, 파장이 작을수록 회절각이 작아지기 때문에 렌즈의 크기가 클수록, 광원의 파장이 작을수록 R이 작아집니다.
이로써 공식이 하나 탄생하게 됩니다.
R=k1*(빛의 파장/NA)
따라서 빛의 파장(란다)이 작을수록, 렌즈의 크기(NA)가 클수록 R값은 작아집니다.
*k1은 공정상수로 반도체 회사마다 공정기술에 따라 달라집니다. 이러한 공정상수에 해당하는 해상도를 향상하는 기술은 다음 글에 후술 하겠습니다.

초점심도(DOF : Depth of Focus)
햇갈리실까봐 DOF가 있는 위 그림을 다시 한번 가져와 봤습니다. DOF란 렌즈의 초점으로부터 얼마만큼 유효한 상을 얻을 수 있는지를 나타내는 척도 입니다. 예를 들어 보겠습니다. wafer위 PR에 빛을 조사하기 위해 지금 Expose공정이 진행되고 있습니다. PR의 두께를 10 nm라고 가정하겠습니다. 그러고 초점이 PR의 중간에 맺쳐지고 DOF가 10 nm라면 초점 위로 +5 nm, 아래로 -5 nm가 DOF범위이니 10 nm두께 전부에 빛을 조사시킬 수 있습니다.

좀 더 이해가 쉽게 가고자 렌즈가 큰 경우, 작은 경우를 극단적으로 비교해 보겠습니다. 왼쪽 그림처럼 렌즈가 큰 경우 PR내로 들어가는 각도 세타값이 커집니다. 세타가 크다는 뜻은 초점 위, 아래로 빛의 범위가 넓어져서 정확한 상이 맺히기 힘들다는 뜻입니다. 이는 따라서 DOF의 감소를 의미합니다. 반대로 렌즈가 작으면 DOF가 커져 PR 10 nm범위에 충분히 빛을 조사시킬 수 있게 됩니다.
정리하자면 DOF는 wafer기준으로 수직방향으로 얼마만큼 유효한 상을 얻을 수 있는지를 나타내는 수치이며 DOF는 클수록 좋습니다. 이는 위에서 보셨다시피 렌즈의 크기가 작을수록 좋고, 파장도 클수록 좋습니다.
*파장이 짧으면 에너지가 커 매질에 쉽게 흡수되어 버립니다. 따라서 파장이 클수록 DOF여유도가 증가합니다.
최종 정리하자면 DOF는 수직방향으로의 해상도, Resolution은 수평방향으로의 해상도를 의미합니다.
Resolution = k1*(파장/NA), DOF = k2*(파장/NA^2)
여기서 문제가 발생합니다. Resolution은 작을수록 좋고, DOF는 클수록 좋은데 위 식이 분자, 분모다 같습니다.
렌즈의 크기(NA)를 키우면 R은 작아져 좋으나 DOF는 작아져 안 좋아지는 것이죠. 파장도 줄이면 R은 작아져 좋으나 DOF는 작아져 안 좋아집니다. 이를 영어로 Trade-off 관계라고 합니다.
다음 글로는 본격적으로 위에서 살펴본 Trade-off관계에 있는 Resoluton, DOF를 개선하는 기술에 대해 알아보겠습니다.
위 공식에서 공정상수인 k1, k2에 해당하는 기술이기도 합니다.
(CMP, 단파장, immersion(액침노광), PSM, OPC)
'반도체 8대공정 > photolithography' 카테고리의 다른 글
| 1-8 photolithography(포토리소그래피) 공정_PEB (0) | 2021.01.03 |
|---|---|
| 1-7 Expose(3)_해상도 개선 기술 (2) | 2021.01.02 |
| 1-5 photolithography(포토리소그래피) 공정_Expose(1) (0) | 2020.12.31 |
| 1-4 photolithography(포토리소그래피) 공정_Soft Bake (0) | 2020.12.30 |
| 1-3 photolithography(포토리소그래피) 공정_PR Coating (0) | 2020.12.23 |



댓글